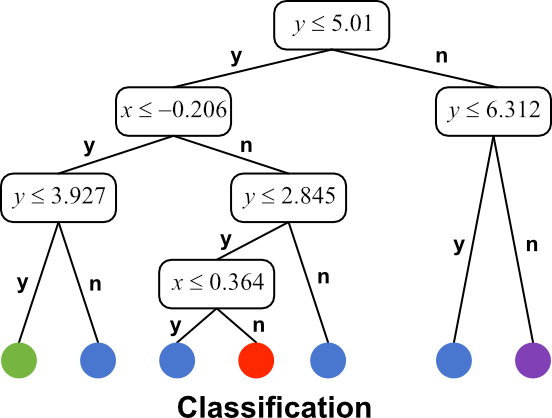
Data classification
using decision trees
Data classification is a supervised learning method that seeks to classify a datapoint based on its similarity to other, known datapoints that have been used to train the system. As with cluster analysis there are many methods, one of which, a decision tree, is shown here.A decision tree classifies data by asking a series of questions to which the answer can only be yes or no. These can be numerical, for example is the value less than 4, etc., or categorical, for example is it red? Through a series of questions produced by the decision tree training algorithm the best categorical fit to the new data point is predicted. A simple example is shown below that attempts to classify an animal based on four animals it knows about.
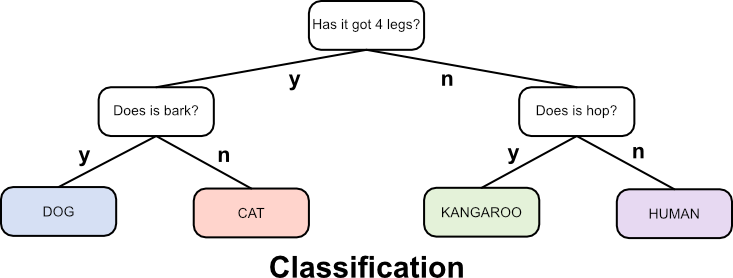
The above example asks two questions based on three given attributes of an animal, i.e. how many legs is has, whether it barks or not, and whether it hops. It uses these to find the best set of questions to ask to identify the animal. Obviously this is a very simple example but it highlights the algorithmic requirements to produce a decision tree:
-
Given a set of data that has measured attributes and a known category:
- For each attribute find the question that partitions the data in the best way to identify a category.
- Choose the best question identified above and use it to make the first partition.
- Repeat on each sub-partion to find the next best question to ask.
- Carry on repeating until all training entries are categorised satisfactorily.
For the algorithm to work, a measure of the information gained by asking each question is required. This is obtained by looking at each possible split between attribute points for each possible attribute and measuring how homogeneous it is. The split with the best homogeneity is chosen at each step.
In physics entropy is a term that describes the amount of disorder in a system. Low entropy is
associated with things being highly ordered and uniform, while high entropy signifies more disorder.
For the problem of producing a decision tree, entropy can be used to measure how pure a set of points
in a region, \(\mathbf{X}\), is, as defined as follows:
$$ S(\mathbf{X}) = - \sum_{i=1}^{k} P(c_i | \mathbf{X}) log_2 P(c_i | \mathbf{X}),$$
where \(P(c_i | \mathbf{X})\) is the probability that a point of class \(c_i\) is in the region
\(\mathbf{X}\), and \(k\) is the total number of classifications. The value of \(P(c_i | \mathbf{X})\)
can be estimated by counting the fraction of points in \(\mathbf{X}\) that are of class \(c_i\).
When \(P(c_i | \mathbf{X})=0\) the summation contribution is taken as zero.
If the region contains only points of a single class, \(c\) then \(P(c_{i=c} | \mathbf{X})=1\) and
\(P(c_{i\neq c} | \mathbf{X})=0\), and the entropy is zero. For all other cases (except where
\(\mathbf{X}\) contains no points at all), \(S > 0\).
The split entropy gives a weighted average of the entropies of the two regions created when a split is made (this split gives the question to ask in the decision tree) as: $$ S(\mathbf{X_Y},\mathbf{X_N}) = \frac{n_y}{n}S(\mathbf{X_y})+\frac{n_N}{n}S(\mathbf{X_N}), $$ where \(\mathbf{X_Y}\) is the region of answering yes to the split question, \(\mathbf{X_N}\) is the region of answering no to the split question, \(n\) is the number of points in \(\mathbf{X}\), \(n_Y\) is the number of points in \(\mathbf{X_Y}\) and \(n_N\) is the number of points in \(\mathbf{X_N}\).
The above expressions can now be used to define the information gain as a result of the split as $$ I_G(\mathbf{X},\mathbf{X_Y},\mathbf{X_N})=S(\mathbf{X})-S(\mathbf{X_Y},\mathbf{X_N}). $$ The higher the information gain, the better the split point is at producing more homogeneous regions. This measure is used in the algorithm to determine at each stage what the best split question is.
The split entropy gives a weighted average of the entropies of the two regions created when a split is made (this split gives the question to ask in the decision tree) as: $$ S(\mathbf{X_Y},\mathbf{X_N}) = \frac{n_y}{n}S(\mathbf{X_y})+\frac{n_N}{n}S(\mathbf{X_N}), $$ where \(\mathbf{X_Y}\) is the region of answering yes to the split question, \(\mathbf{X_N}\) is the region of answering no to the split question, \(n\) is the number of points in \(\mathbf{X}\), \(n_Y\) is the number of points in \(\mathbf{X_Y}\) and \(n_N\) is the number of points in \(\mathbf{X_N}\).
The above expressions can now be used to define the information gain as a result of the split as $$ I_G(\mathbf{X},\mathbf{X_Y},\mathbf{X_N})=S(\mathbf{X})-S(\mathbf{X_Y},\mathbf{X_N}). $$ The higher the information gain, the better the split point is at producing more homogeneous regions. This measure is used in the algorithm to determine at each stage what the best split question is.
The interactive element below takes a set of categorised data that have two attributes based on the (x, y) positions of the point on a plane and produces a decision tree based on it. When started each optimal split is shown and the colours of the resulting regions chosen to represent the category with the maximum count in that region. So, the first split, for example only categorises data into purple and red items.