Transform your data

the good and the bad

Data are not always in the most convenient form to work with and sometimes applying a transformation can help simplify analysis. Transformations can be applied to one attribute or to many. A simple example is given below. The curve on the left represents data captured during a testing process (in this case this curve is typical of the deceleration experienced by objects of different masses but with the same contact area being dropped and cushioned by a foam cushion). A simple data fit model of the behaviour is not apparent for the raw data as the shape is quite complex. However, by taking $log_e$ of the x value, i.e. define $x' = log_e(x)$, and replotting $(x',y)$ values the curve becomes similar in shape to a quadratic which is much easier to work with.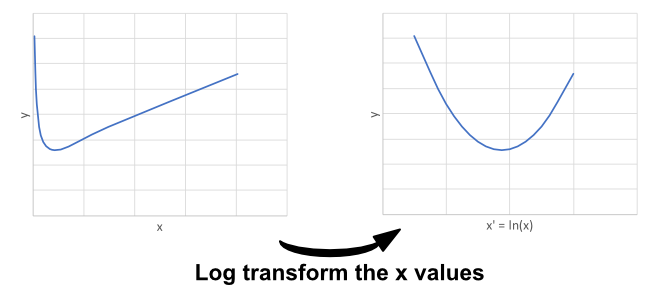

The $log_e$ transform is also useful when working with distributions that have long tails, such as the one shown below-left. Applying the transform shortens the tail and makes the distribution appear more like a normal distribution.

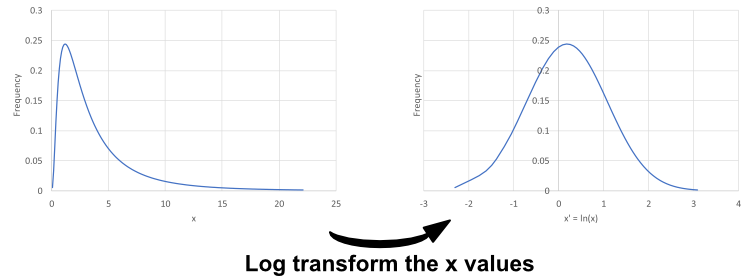
Beware of applying statistical tests on the transformed data as they are not equivalent to statistical tests on the raw data! For example, if you apply $x' = log_e(x)$ and find the mean of $x'$, $\overline{x'}$, then do the reverse transformation, $x=e^{\overline{x'}}$, you will not recover the mean of the original data.

Need more detail? Show the maths

Let X be a set of data points $ \{ x_1,x_2,\cdots,x_n \} $. The arithmetic mean of X, $\overline{x}$, is given by $$ \overline{x} = \frac{1}{n}\sum_{i=1}^n x_i $$ Now construct the $log_e$ transformed set of data points, X'$ =\{ x_1', x_2', \cdots,x_n' \} $ where $ x_i' = log_e(x_i)$. The arithmetic mean of X', $\overline{x'}$, is given by \begin{aligned} \overline{x'} &= \frac{1}{n}\sum_{i=1}^n x_i' \\ &= \frac{1}{n}\sum_{i=1}^n log_e{x_i} \\ &= \frac{1}{n} log_e \left( \prod_{i=1}^n x_i\right) \\ &= log_e \left( \prod_{i=1}^n x_i\right)^{\frac{1}{n}} \end{aligned} Raising $e$ to the power of both sides, $$e^{\overline{x'}} = \left( \prod_{i=1}^n x_i\right)^{\frac{1}{n}},$$ i.e. the inverse transform of $\overline{x'}$ is not the arithmetic mean of X, instead it is the geometric mean of X. Any statistical tests you perform that are related to the arithmetic mean in the transformed data will be tests on the geometric mean in the raw data, and these are very different. Consider the set:

X $= \{1,1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,4,4,5 \}$.

The arithmetic and geometric means of X are 2.6 and 2.271 respectively. Now consider the set

Y $= \{1,1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,4,4,1000 \}$.

The arithmetic and geometric means of Y are 52.35 and 2.959 respectively. Notice how the arithmetic mean is much more sensitive to high skews in the distribution than the geometric mean is.

Taking logs is not the only transformation that can be applied. Others include translations, scaling, rotations, etc. Translations and rotations form an important set of transformations as they allow data to be aligned with the axes in such a way that the axes are along the "principal components" of the data. This is principal component analysis (PCA). First the data are centred so that the mean along any feature axis is zero. The data are then rotated so that the largest variances are aligned with the axes. One great benefit of PCA is that the alignments are constructed in decreasing order of data variance. This means that all the important information could be captured by the first $p$ of $N$ components, where $p$ may be very much smaller than $N$. This results in a reduction of dimensionality and subsequent data analysis is simplifed.

The interactive element below shows the PCA process for a simple set of data where each element has two attributes.