Time to queue

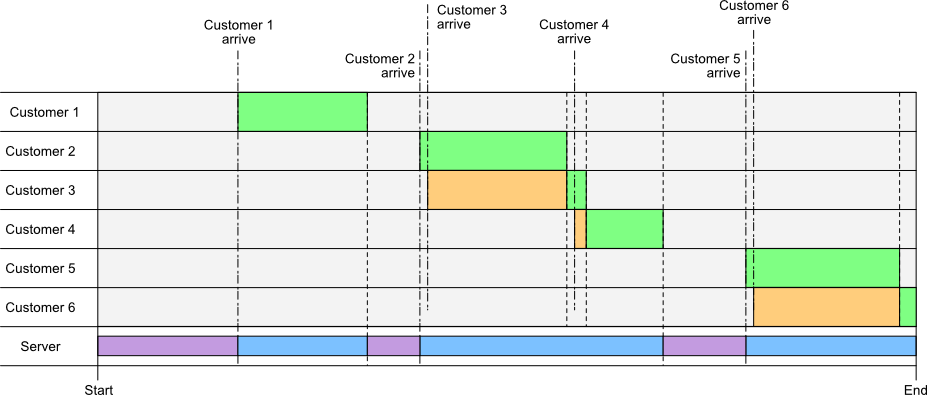
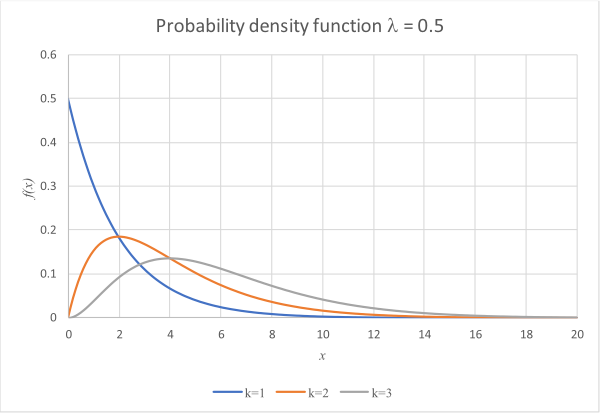
The mathematics in this problem is largely based around statistical distributions. One useful distribution is the Erlang distribution, which is characterised by a shape parameter, \(k\) and a rate parameter, \(\lambda\). When \(k = 1\), the distribution is an exponential distribution, while with larger values the distribution tends towards a normal distribution. The rate parameter determines how fast the distribution drops to zero and the location of the maximum when \(k \geqslant 2\). The larger the value of \(\lambda\), the quicker the distribution drops to zero, and the further to the left the peak value occurs. $$ f(x;k,\lambda )={\lambda ^{k}x^{k-1}e^{-\lambda x} \over (k-1)!}\quad {\mbox{for }}x,\lambda \geq 0$$

The mean of an Erlang distribution is given by $$Mean \left( f(x;k,\lambda \right) = \frac{k}{\lambda}. $$ The Erlang distribution is very useful in queuing problems. The Erlang distribution with \(k=1\) models the inter-arrival time between customers (which are assumed to be indepedndent events). In this case the mean time between arrivals is \(\frac{1}{\lambda}\), so \(\lambda\) represents the mean number of arrivals per unit time. The probability that exactly \(n\) customers arrive in the unit time is given by the Poisson distribution: $$ f (n;\lambda)= \frac{\lambda ^n e^{-\lambda}}{n!}. $$ As an aside, this distribution also models the number of count events measured by a Geiger counter when detecting ionising radiation from radioactive decay.

An Erlang distribution may also be used to model the time it takes to serve a customer. The distribution with \(k=1\) could be used but this allows for very short service times with reasonably high probabilty. In a customer-service situation this may not be realistic as time will be taken to unload at the checkout and for payment to be taken. To allow for this values of \(k \geqslant 2\) may be used. Recall the mean service time is given by \(\frac{k}{\lambda}\), so \(\frac{\lambda}{k}\) is the mean number of customers served per unit time. In the simulation below, \(k=2\), so to serve an average of \(s\) customers per unit time the Erlang distribution with \(\lambda = 2s\) should be used.

To construct a simulation a method of drawing time intervals from the Erlang distribution is required. For the \(k=1\) case the distribution reduces to the exponential distribution $$ f(x;\lambda ) = \lambda e^{-\lambda x} $$ Integrating this between \(x=0\) and \(x=t\) gives the probability that an event will happen within time t. $$P(event) = \int_{0}^{t} \lambda e^{-\lambda x} dx = 1-e^{-\lambda t}.$$ Rearranging, $$ t = -\frac{1}{\lambda} \ln \left(1 - P(event)\right)$$ If the event occurs at random then \(1-P(event)\) can be replaced by a random uniform deviate, U, on the interval (0,1]. This gives a method for generating random exponentially-spaced times between events as $$ t = -\frac{1}{\lambda} \ln U .$$ For the case where \(k \geqslant 2\) the above is generalised using \(k\) uniform deviates as $$ t = -\frac{1}{\lambda} \ln \prod_{i=1}^{k} U_i .$$